- 规律性问题 在平面上画20个圆,问这20个圆最多可能将平面分为多少个部分? 答案详见第二页 解: 分析 直接画出20个圆去数当然是行不通的.先考虑一些简单的情况: 一个圆最多分平面为2部分; 二个圆最多分平面为4部分; 三个圆最多分平面为8部分; 当第二个
规律性问题
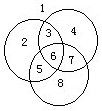
在平面上画20个圆,问这20个圆最多可能将平面分为多少个部分?
答案详见第二页
解:分析 直接画出20个圆去数当然是行不通的.先考虑一些简单的情况:
一个圆最多分平面为2部分;
二个圆最多分平面为4部分;
三个圆最多分平面为8部分;
当第二个圆在第一个圆的基础上加上去时,第二个圆应与第一个圆有2个交点,这两个交点将新加的圆分为2段,其中每一段弧都将所在平面部分一分为二,所以所分平面部分数在原有2部分的基础上又增添2部分.同样道理,三个圆最多分平面的部分数是在2个圆分平面为4部分的基础上又增加4部分.
继续前面的分析过程,画第20个圆时,与前19个圆最多有19×2=38个交点,第20个圆的圆弧被分成为38段,也就是增加了38个区域,所以20个圆最多分平面的部分数为:
2+1×2+2×2++19×2
=2+2(1+2+3++19)

规律性问题(六年级奥数题及答案).doc
2024-06-25 点击次数: 上传者:青葱岁月 下载全文
猜你还喜欢
-
2023六年级数学上册 三 分数除法 3 探索规律作业课件 西师大版
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:8
- 2023六年级数学上册 三 分数除法 3 探索规律作业课件 西师大版 ...
-
2023六年级数学上册 三 分数除法 3探索规律上课课件 西师大版
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:6
- 2023六年级数学上册 三 分数除法 3探索规律上课课件 西师大版 ...
-
2023六年级数学上册 三 分数除法 3探索规律作业课件 西师大版
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:9
- 2023六年级数学上册 三 分数除法 3探索规律作业课件 西师大版 ...
-
2023六年级数学上册 三 分数除法 3探索规律作业课件1 西师大版
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:9
- 2023六年级数学上册 三 分数除法 3探索规律作业课件1 西师大版 ...
-
2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体上课课件
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:3
- 2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体上课课件 苏教版 ...
-
2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体作业课件
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:9
- 2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体作业课件 苏教版 ...
-
2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体作业课件
- 所属分类:范文资料
- 更新时间:2024-12-05
- 点击次数:4
- 2023六年级数学上册 一 长方体和正方体探索规律 表面涂色的正方体作业课件苏教版 ...
-
2023五年级数学上册 二 小数乘法 1小数点位置变化第1课时 小数点位置向右移
- 所属分类:范文资料
- 更新时间:2024-12-04
- 点击次数:2
- 2023五年级数学上册 二 小数乘法 1小数点位置变化第1课时 小数点位置向右移动的规律上课课件 冀教版 ...
-
2023五年级数学上册 二 小数乘法 1小数点位置变化第2课时 小数点位置向左移
- 所属分类:范文资料
- 更新时间:2024-12-04
- 点击次数:4
- 2023五年级数学上册 二 小数乘法 1小数点位置变化第2课时 小数点位置向左移动的规律上课课件 冀教版 ...
-
2023五年级数学上册 二 图形的平移、旋转与轴对称 5 探索规律作业课件 西师
- 所属分类:范文资料
- 更新时间:2024-12-04
- 点击次数:9
- 2023五年级数学上册 二 图形的平移、旋转与轴对称 5 探索规律作业课件 西师大版 ...